算法概述 - 算法复杂度 - 时间复杂度与空间复杂度

一、算法概述

算法，简单来说，就是解决特定问题的一系列明确且有限的指令。它就像是一份烹饪食谱，告诉厨师（计算机）如何一步一步地将原材料（输入数据）转化为美味的菜肴（输出结果）。

在计算机科学中，算法无处不在。比如，搜索引擎在海量网页中快速找到你需要的信息，电商平台根据你的浏览历史推荐你可能喜欢的商品，这些背后都离不开精心设计的算法。

以排序问题为例，我们需要将一组无序的数据按照从小到大或从大到小的顺序排列。有很多种算法可以解决这个问题，像冒泡排序、插入排序、快速排序等。这些算法就像是不同的烹饪方法，虽然都能做出排序这道“菜”，但在效率和适用场景上各有不同。

二、算法复杂度的重要性

当我们面对多种算法来解决同一个问题时，如何选择最合适的算法呢？这就需要用到算法复杂度的概念。算法复杂度是衡量算法优劣的重要指标，它主要分为时间复杂度和空间复杂度。通过分析算法复杂度，我们可以预估算法在处理不同规模数据时所需的时间和空间资源，从而选择出效率最高、最适合当前场景的算法。

想象一下，你要从一个城市到另一个城市，有多种交通方式可供选择，如步行、骑自行车、坐汽车、坐飞机等。不同的交通方式在时间和成本（这里可以类比为算法的时间和空间复杂度）上有很大差异。如果你要去的地方很近，步行可能是个不错的选择；但如果要去很远的地方，坐飞机显然更节省时间。同样，在算法选择中，我们也需要根据问题的规模和实际需求来权衡时间和空间的开销。

三、时间复杂度

定义

时间复杂度是指算法执行所需要的计算工作量，它反映了算法执行时间随输入规模增长而增长的趋势。通常用大 O 符号来表示。大 O 符号描述的是算法在最坏情况下的时间复杂度，它忽略了常数项和低阶项，只关注最高阶项。

常见时间复杂度及示例

$O(1)$ - 常数时间复杂度

无论输入规模多大，算法的执行时间都是固定的。例如，访问数组中的一个元素：

arr = [1, 2, 3, 4, 5]
print(arr[2])  # 直接访问数组的第 3 个元素，时间复杂度为 O(1)
#### $O(log n)$ - 对数时间复杂度
随着输入规模的增大，算法的执行时间呈对数级增长。常见于二分查找算法：
```python
def binary_search(arr, target):
    left, right = 0, len(arr) - 1
    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9]
target = 5
print(binary_search(arr, target))  # 二分查找，时间复杂度为 O(log n)

$O(n)$ - 线性时间复杂度

算法的执行时间与输入规模成正比。例如，遍历数组中的所有元素：

arr = [1, 2, 3, 4, 5]
for num in arr:
    print(num)  # 遍历数组，时间复杂度为 O(n)

$O(n log n)$ - 线性对数时间复杂度

常见于一些高效的排序算法，如快速排序、归并排序：

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])
    return merge(left, right)
def merge(left, right):
    result = []
    i = j = 0
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    result.extend(left[i:])
    result.extend(right[j:])
    return result
arr = [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5]
print(merge_sort(arr))  # 归并排序，时间复杂度为 O(n log n)

$O(n^2)$ - 平方时间复杂度

算法的执行时间与输入规模的平方成正比。例如，冒泡排序：

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
    return arr
arr = [3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5]
print(bubble_sort(arr))  # 冒泡排序，时间复杂度为 O(n^2)

时间复杂度对比表格

时间复杂度	描述	示例算法
$O(1)$	常数时间，执行时间固定	访问数组元素
$O(log n)$	对数时间，执行时间随输入规模对数增长	二分查找
$O(n)$	线性时间，执行时间与输入规模成正比	数组遍历
$O(n log n)$	线性对数时间，高效排序算法常见复杂度	快速排序、归并排序
$O(n^2)$	平方时间，执行时间与输入规模平方成正比	冒泡排序、插入排序

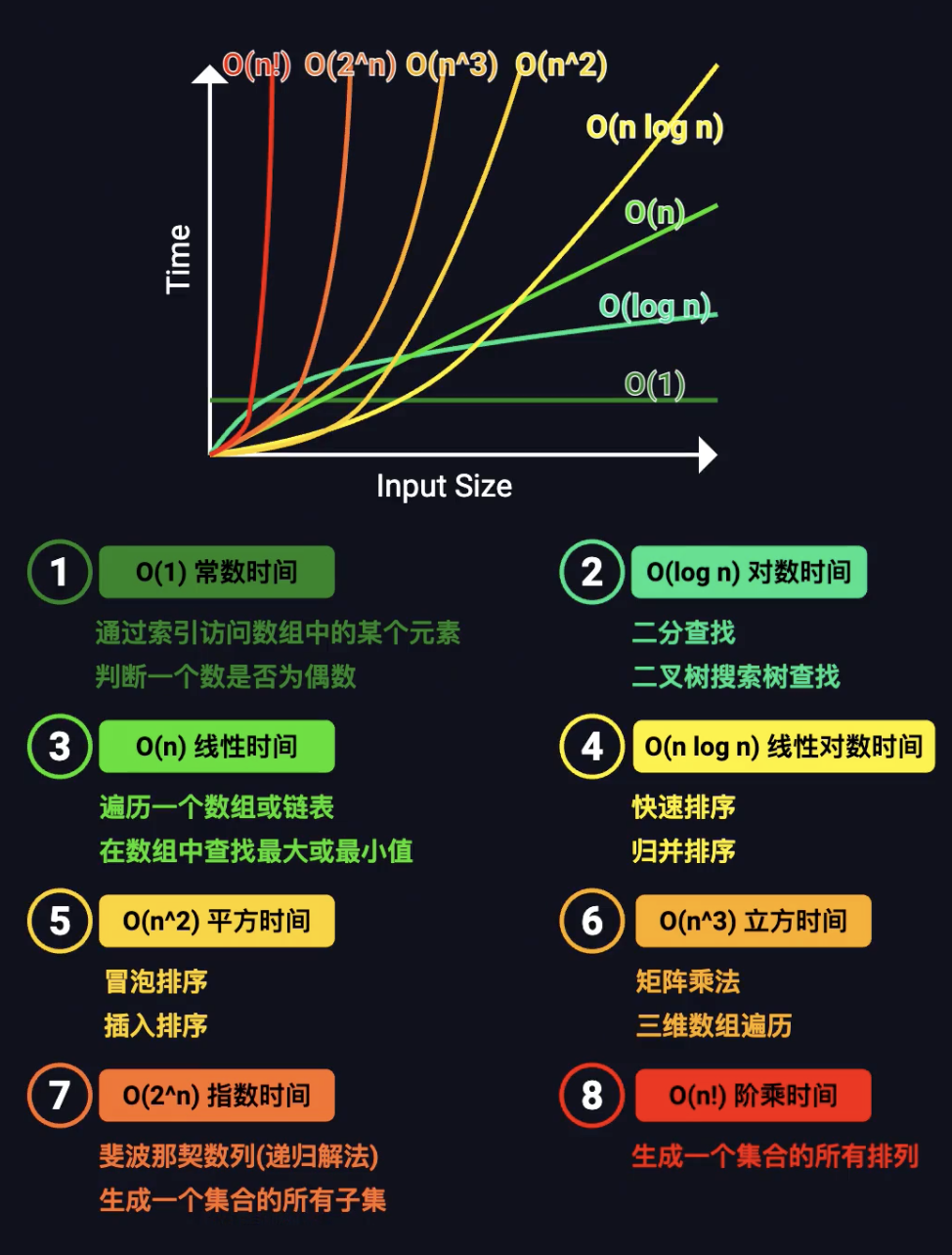
图来自波波微课

四、空间复杂度

定义

空间复杂度是指算法在执行过程中所需要的存储空间，它反映了算法所需存储空间随输入规模增长而增长的趋势，同样用大 O 符号表示。

常见空间复杂度及示例

$O(1)$ - 常数空间复杂度

算法所需的存储空间不随输入规模的变化而变化。例如，交换两个变量的值：

a = 1
b = 2
a, b = b, a  # 交换变量值，只使用了常数级的额外空间，空间复杂度为 O(1)

$O(n)$ - 线性空间复杂度

算法所需的存储空间与输入规模成正比。例如，创建一个与输入数组长度相同的新数组：

arr = [1, 2, 3, 4, 5]
new_arr = [i * 2 for i in arr]  # 创建新数组，空间复杂度为 O(n)

$O(n^2)$ - 平方空间复杂度

算法所需的存储空间与输入规模的平方成正比。例如，创建一个二维数组：

n = 5
matrix = [[0] * n for _ in range(n)]  # 创建二维数组，空间复杂度为 O(n^2)

五、总结

时间复杂度和空间复杂度是衡量算法性能的两个重要指标。在实际应用中，我们通常需要在时间和空间之间进行权衡。有时候，我们可以通过增加空间开销来减少时间开销，反之亦然。

例如，在一些缓存算法中，我们会使用额外的存储空间来存储已经计算过的结果，这样下次需要相同结果时可以直接从缓存中获取，从而减少计算时间。而在一些对存储空间要求严格的嵌入式系统中，我们可能会选择空间复杂度较低但时间复杂度较高的算法。

通过对算法复杂度的分析，我们可以更好地理解算法的性能特点，选择合适的算法来解决实际问题，提高程序的效率和性能。希望本文能帮助你更好地理解算法复杂度的概念，在编程实践中做出更明智的选择。

.bat程序教程	python入门基础教程	Pandas教程	Pygame教程
Django3.2.9教程	Flask1.1.1教程	python3.X - 区块链教程	Java教程
Spring教程	C#教程	PHP教程	R教程
Node.js教程	mysql数据库教程	Redis数据库教程	MongoDB数据库教程
RabbitMQ教程	Lua教程	FindBI教程	HTML5教程
CSS教程	Javascript教程	jQuery教程	微信小程序教程
微信小游戏教程	Vue.js教程	服务器教程	TensorFlow教程
PyTorch教程	Unity教程	Objective-C教程	Android教程
AppleScript教程	Mac - SHELL教程	算法教程	Python教程
数据库教程	运维工具教程	Nginx教程	Docker教程

算法概述 - 算法复杂度 - 时间复杂度与空间复杂度